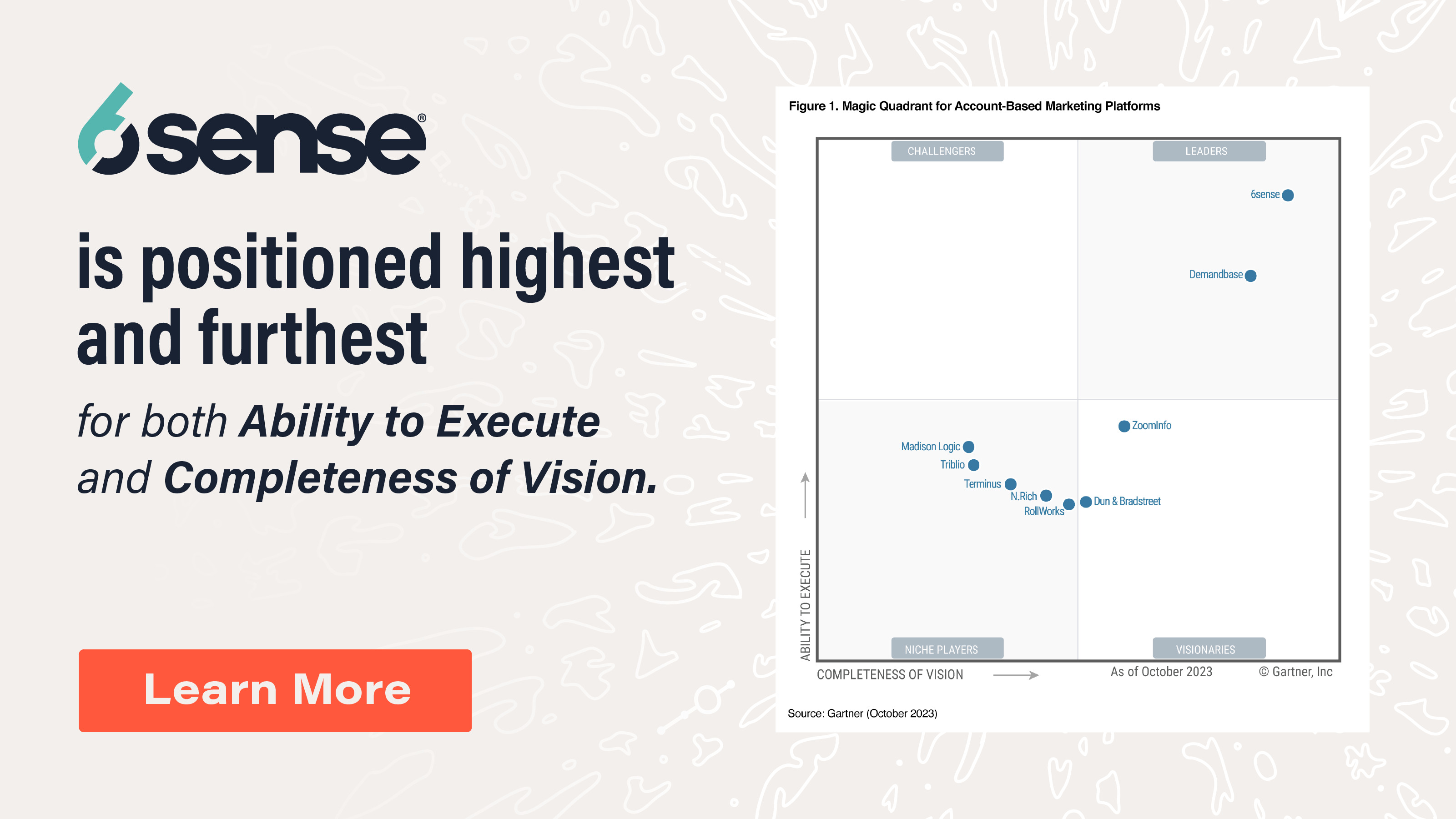
Z-scores are a more sophisticated form of centering. Z-scores further refine centering to allow researchers to compare measures on questions or assessments that were taken using different response scales.
Say for example, that you have just discovered that new colleagues from a recent acquisition collected customer satisfaction data from their customers using 5-point scales. You have been doing the same survey with your customers, but you have used a 7-point scale. You would love to compare satisfaction between the two, but how can you when they used different scales?
The answer is by using z-scores. Centering places each response, regardless of the scale, in exact relation to the center, or average, of the response set. Z-scores go one step further and divide that centered value by the standard deviation for the data set. This yields a value that is a precise measurement of how far each value is from the average, and it states it in terms of how much variability there was in the data set – the standard deviation. It’s technical, but it really works.
Once z-scores have been calculated for both datasets, they can be safely compared, by, for example, using a T-test to evaluate whether the average ratings for the two surveys was different.