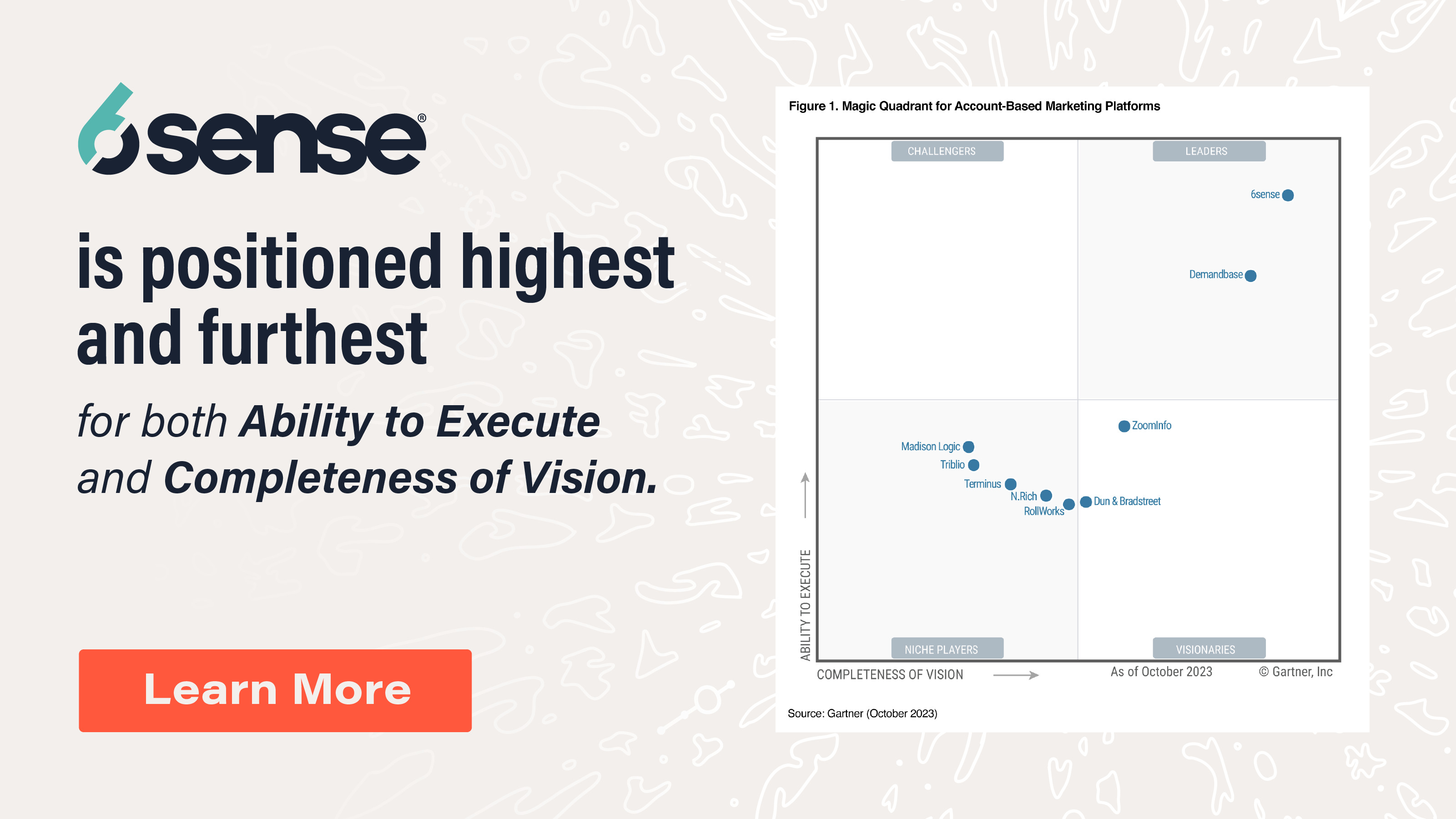
Whenever we take measurements of things in the real world, there are factors that impact that measurement that we cannot account for. In surveys where we are asking participants to report about what they know or believe, the same person might answer a question somewhat differently on different occasions. When measuring sales performance for a given quarter, some sellers may be experiencing either good or bad luck at any given time that is not related to how well they typically perform.
Researchers call this unmeasured variability “measurement error.” There are two primary ways this error is measured.
Standard Error
The standard error measures the potential variability between the average of a dataset and the true average of the entire population you want to understand.
Imagine you want to know how far employees in your company live from the office based on their department. Instead of asking everyone, you pick some employees from each department at random and measure how far they live from the office. Imagine that there is very little variability in how far the employees you sampled live from the office – they all live within just a few blocks of the office. Measuring their average distance would yield an average, and each individual you measured would be found at a distance very close to the average. For this set of measurements, the standard error in the measurement would be quite low.
If, on the other hand, you found a wide range of distances. Some lived within a block and some lived dozens of miles from the office, you might end up with the same average distance for your sample, but there would be a larger standard error. And, if you picked any given employee at random, you would be less certain that this employee lived at about the same distance from the office as the average.
Standard error helps us know how reliable our sample is for estimating what’s true for the whole group. If it’s small, we’re more confident in our sample; if it’s large, we’re less sure.
Standard Deviation
Standard deviation measures how spread out a group of measurements is from the average, and therefore how much variability there is within the data set. Standard deviation helps us understand how much the measures within a group differ from each other.
In the example above, standard error measures how far from the office a new person that we survey would expect to live. The standard deviation measures how far the individuals we have already measured were on average.
The standard deviation is a critical tool for researchers and allows researchers to perform many useful data transformations, such as centering a variable and creating z-scores.