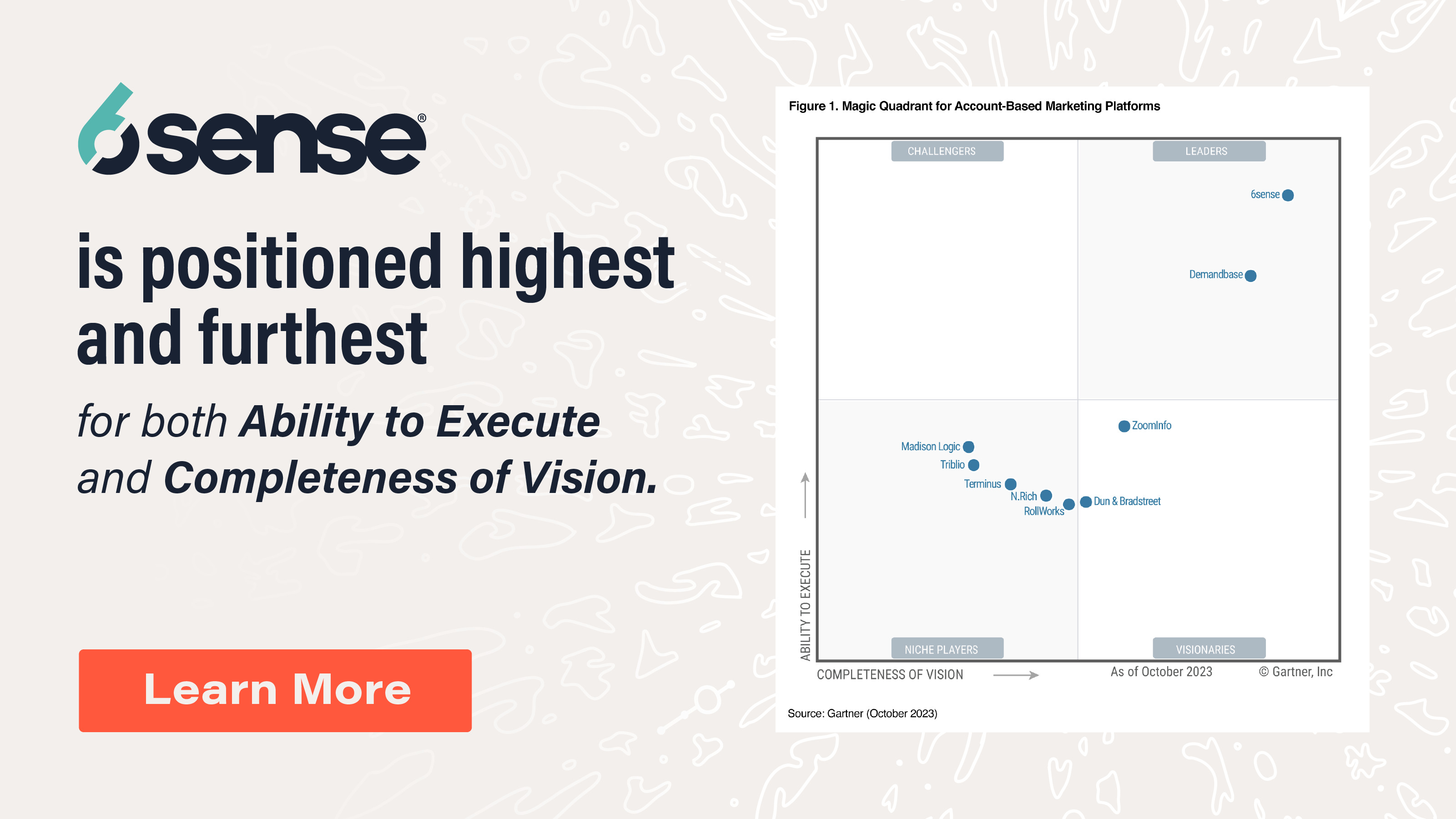
Logistic regression is like multiple regression, but is used when the outcome variable is binary (e.g., yes/no, win/loss, made quota/did not). Like multiple linear regression, logistic regression allows us to test the influence of multiple factors on the outcome variable. Logistic regression is used across many industries and scenarios, from predicting which accounts will purchase to which patients will survive a treatment.
Where multiple linear regression provides a model to tell us how much of the change or difference in an outcome variable is due to the factors we have entered into the model, the results from logistic regression instead tell us how the factors in a model increase or decrease the odds of one of the two potential outcomes happening.
For example, if we wanted to test the impact of marketing campaigns on the likelihood of a prospect account becoming a sales opportunity, we would include the following variables as factors in the model, with a binary variable – Became An Opportunity – as the outcome variable.
Independent variable 1: Marketing campaign 1: number of touches per account
Independent variable 2: Marketing campaign 2: number of touches per account
Independent variable 3: Marketing campaign 3: number of touches per account
Independent variable 4: Marketing campaign 4: number of touches per account
Outcome variable: Became an opportunity: Yes or No
The logistic regression model would return two primary results:
- A percentage representing the proportion of the likelihood of an account becoming an opportunity that the entire model explains. In other words, if we have these variables for a set of accounts, how much of the likelihood of becoming an opportunity can we predict?
- How each variable in the model increases or decreases the likelihood of an account becoming an opportunity. For example, we might find that being touched by Marketing Campaign 4 increases the likelihood (odds) that an account becomes an opportunity by 3%.
In our own B2B Buyer Experience Research we used logistic regression to predict whether buyers would use outside help, such as industry experts and consultants, to help them make a purchase. Using data we collected about them – such as how many vendors they considered, the cost and type of what they’re buying, and how long it takes them to make a purchase – we built a model that predicted with 83% accuracy whether other buyers would utilize outside resources or not.