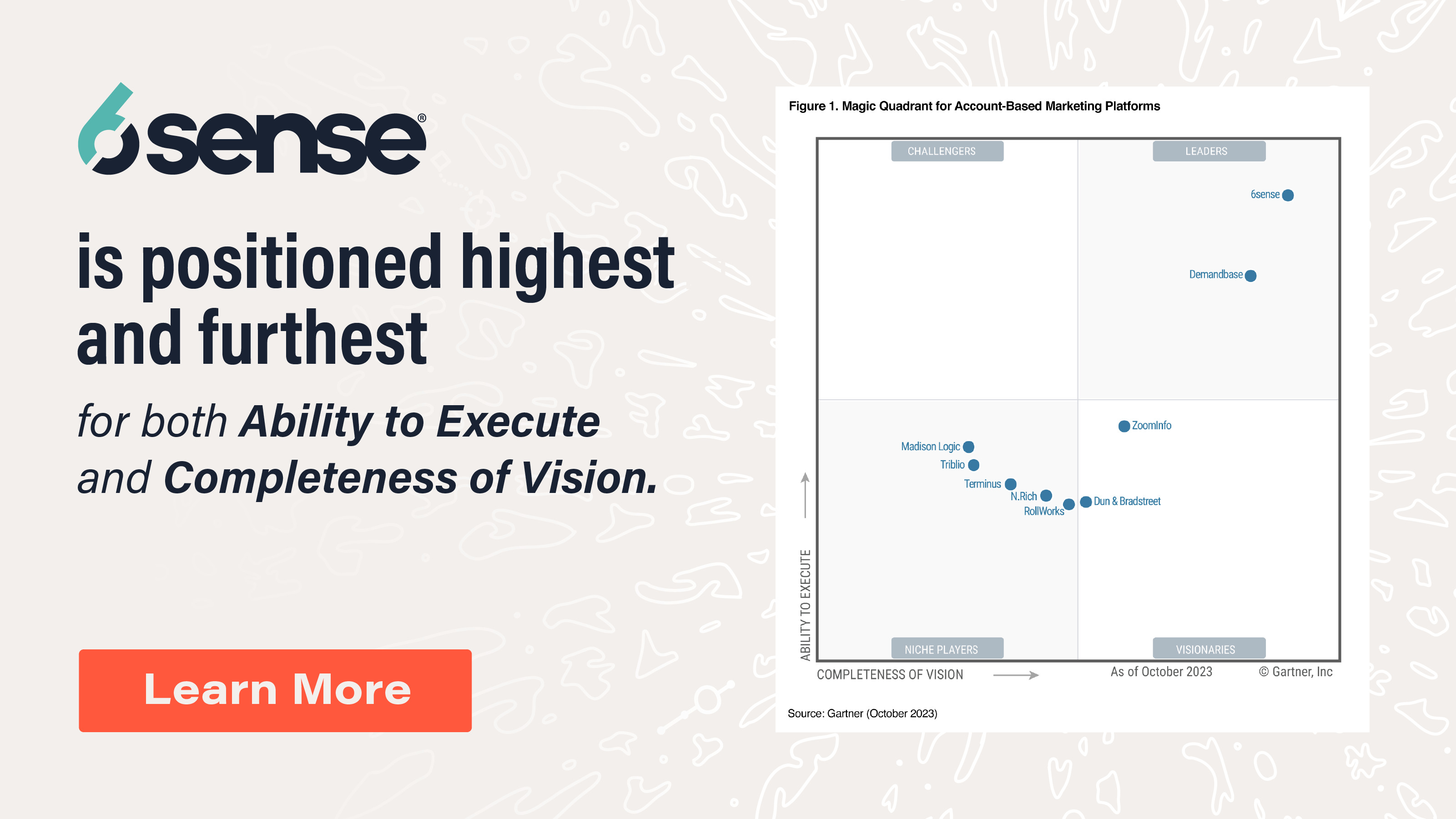
When we measure a sample of anything, we end up with an exact number, typically an average of whatever we have measured (e.g., 4.5 opportunities produced per BDR per month). That number often seems very precise, and for the sample we measured, it is. But if we wanted to know what to expect going forward if we continue measuring, or if we measured a different sample, we would not expect to find exactly the same average. In the above example, we would not expect to find that a new group of BDRs produced exactly 4.5 opportunities. Nor would we expect that any given BDR would have produced 4.5 opportunities.
Instead, what we can say is that future monthly measures will likely fall within a relatively small range around that precise average. In statistics, that likely range can be computed mathematically and is called the confidence interval.
Think of a confidence interval, then, as a “likely range.” It tells us where we would probably find the answers most of the time if we were to survey a new but similar sample from a population.
For example, in a recent survey, we saw that buyers in IT departments found their interactions with vendors a bit more useful than non-IT buyers, giving them an average rating of 4.1 out of 5. The T-test that measures the difference between IT and non-IT buyers returned a p-value of p < .001. This means that there is less than a .1% chance that we will find something different if we repeat the study with a similar audience – a highly reliable finding.
But that does not mean we would expect to find future IT buyers to rate vendor helpfulness at exactly 4.1 out of 5. Instead, we would look to the confidence interval to give us a range of values within which we would expect to find the new measures.